After trying to understand physics through popsci media, I decided to look at the mathematics a bit more, to see what they represent. After looking a bit into relativity, I wonder: what would happen if a system would somehow reach the speed of light? Of course, such a feat is not only impossible in real life, as the speed of light can never be achieved by any particle of mass, but also in mathematics in mathematics, where the speed of light would result in a Lorentz factor that is a division by zero. But what if a system could somehow achieve the speed of light? In this article, I want to describe something that I could not find anywhere, and that is the relation between parallelness, conservation of information, and their mathematical equivalence.
Imagine two particles interacting with each other. The collide head-on and the bounce of each other in opposite direction.

Now imagine a force applied equally to both particles perpendicular to this motion. Let’s call this force a system force, being a force applied equally to both particles. The particles would accelerate in that direction, but would also continue to collide with each other laterally.
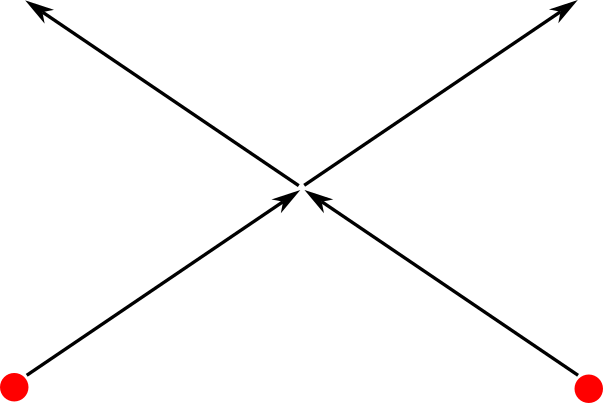
From the original reference frame, the particles will still interact, but farther away. From a reference frame moving along with these particles, it would seem as if these particles are just interacting with each other like in Figure 1.
No system force can make these two particles not interact.
The stronger the force, the faster the particles will move in the direction of the applied force, and the further away they will interact. At the same time, no force can make these particles go faster than the speed of light. The angle at which the particles will interact will get smaller and smaller, as the particles will travel through space more and more parallel to each other, from the perspective of the original reference frame, but they will never be parallel.
As the force becomes bigger, and the particles get closer and closer to the speed of light, time dilates in this two particle system. The more we accelerate these particles, the longer it will take for them to interact.
So it seems to me that if a magic force would be applied to these two particles that makes them reach the speed of light somehow, they would move at the speed of light parallel to each other, as both particles would “fully embrace” the direction of the magic force giver. The result would then not be so special. Just two particles illegally travelling at the speed of light, parallel to each other.
Time dilation would slow down time to zero, as these two particles would never interact.
What is more interesting is thinking about what this means for the information in the universe. Before, no system force could make these two particles not collide. Some outside force, only applied to one of the particles, could make them not collide, but then that outside particle would just carry the information with it. Our system would die, but the information would not be lost. However, if these two particles could achieve parallelness just by applying a system force on them, then the information of their interaction would be lost forever. No system force can now ever make them come together again. Also, in all reference frames, the two particles are travelling parallel to each other. There is no more disagreement about the angle of interaction.
If we would decelerate these two particles to sub-light speed, then they would still be parallel. This is true for all parallel travelling particles in the universe. No system force can make these two particles not be parallel. Therefore, the information of the interaction between our two particles is permanently lost. Before, we could speed up these two particles, or slow them down in any way below the speed of light, and they would always collide. And now they never will. And since they will never collide ever again after any system force, time continues to stop, no matter how fast the system is going. It is almost as if the particles lost a dimension.
The linear algebra of space-time diagrams
I will not get in to deeply into the linear algebra of space-time diagrams, as I only half-understand myself. I just want to point one thing out about the zero division in the Lorentz factor in case of the speed of light being achieved. It seems to me that 2 dimensions would collapse into 1 dimension, being a line at 45 degrees, after such a Lorentz boost, even though strictly speaking it is undefined. The reason I think this is obvious. As the Lorentz factor reaches infinity, space-time “stretches” more and more into a 45 degree line. It seems logical to assume a full collapse into that line, even tough it is strictly speaking not possible.
The intriguing thing of such a collapse is that no equation can re-map the vectors that ended up on that line. Since multiple vectors end up in the same point on that line, no equation can distinguish them. Before, it did not matter what Lorentz boost you used in whatever direction. As long as it was sub-light speed, the universe would “remember”. But if it collapses into a line, we no longer know what collapsed where. This seems familiar. What was the original angle between our two particles before they reached the speed of light? And how do we get them back together again?
It is nice to see that the mathematics and reality are so in line with each other. They both forbid faster than light travel, and they both seem to suggest the same result if it would happen: you lose knowledge, and your system ends up in a static, parallel form, equal in all reference frames, with no time, a state that no system force (equation) can get you out.
So, what would happen if you could go faster than light?
Tachyons and “time travel”
What would happen if some sort of “tachyonic force” would be applied to the particles that can make them go faster than the speed of light? Well, it depends on what the tachyonic force would be, and how particles would interact with them. If particles would still angle the same way they do in our current understanding when accelerated, and “fully embrace” the force’s direction at the speed of light, than the tachyonic force will just propel them parallel to each other faster than the speed of light. If the interaction between force an particle is different, then I would argue that the angles would move up-to parallel the closer the particles would get to the tachyonic force’s “maximum velocity”, whatever that may be. The information of interaction would then be held, even at velocities above the speed of light, though would be lost if the particles become parallel at the tachyonic force’s maximum velocity.
What would not happen, or so it seems to me, is what might easily happen if you are not careful in the mathematics. It is the notion that the particles, after reaching parallelness, would somehow diverge after a tachyonic force is applied. This, to me at least, makes no sense, Why would a particle do anything other than follow more and more the direction of a force the stronger the force gets? Surely, it would not diverge. Why would it? So, the below depicted interaction would not happen. And yet, we can see in this depiction a notion of time travel.
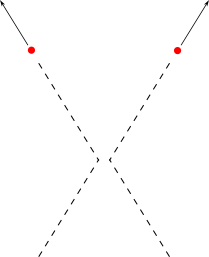
It is as if these particles, that never interacted, interacted in the past. If particles, after some sort of tachyonic force would make them divirge in their angles, then that would represent a form of time travel, in a way. The information that goes out to the universe after the evaporation of our two particle system, is as if these two particles interacted in the past, even though they didn’t.
Strange as this property of divergence would be, if the two particles would be decelerated, then it would logically follow that they would converge again. When particles travel parallel to each other, they would somehow have to remember what angle they were interacting with before they went parallel. Before, the particles weren’t really aware of their angle of interaction. They just were acted upon by a force equal to both. It is this idea of a system force that made them always collide, not some sort of knowledge that the individual particle had. So why, after deceleration opposite to its momentum, would the particle suddenly make an angle? How would each particle remember each “role” before the acceleration to the speed of light? The two particles are equal to each other. Why would one angle “to the left” and the other “to the right” after deceleration? But if it would be able to remember such a thing, then information would not be lost. This “time travel” and divergence idea doesn’t seem to work.
The reason that I mention it, is that there is an idea of “time travel” in physics. Tachyons in space-time diagrams can, under certain conditions, time travel in certain reference frames. Though my understanding of physics is not big enough to properly understand, I wonder to what degree this has something to do with this divergence property.
In Feynman diagrams, positrons are depicted as time travelling electrons.
Positrons in Feynman diagrams
I do not know enough about physics to understand the full potential of Feynman diagrams. But I have noticed that positrons are depicted as “time travelling” electrons. It is important to note here, that Feynman diagrams are representations of equations, and that you need multiple diagrams to make useful predictions. I just want to focus on, from this very limited perspective, that I am not surprised that a positron is a “time traveling” electron, and that flipping the diagrams to “turn positrons into electrons” works.
The nature of a positron is that it is in everything the opposite of its brother, the electron. If, and I hope I say this correctly, a positron-electron pair is created, they move in opposite angles, with exactly the same velocity. The notion that I want to make here, of course, is that the positron behaves as a diverging electron, as described in the “time travel” segment above, as its angle is always opposite to that of its brother at creation, relative to the original momentum that created the pair. I don’t want to go beyond this simple notion, as I do not understand quantum physics at all, but I will remember this in my further studies in physics.
Your freezer as the time machine
The notion that parallelness slows down time is not just limited to the speed of light. You put frozen vegetables in the freezer as you didn’t want the particles of the vegetables to interact as much with each other and the outside world, thereby preventing their decay. In a way, you slowed down time by making the particles of your vegetables move as parallel to each other through space as you possibly could. In a way, your freezer is a time machine.
Conclusion
Time, angles and parallelness seem to be different ways of saying a similar thing. The more parallel a system is relative to some other reference frame, the more time dilated it is.
If a system reaches the speed of light hypothetically, then the particles of that system would, in line with mathematics, travel through space in a parallel trajectory to each other, a state which no system force or equation could undo. Time would slow down to zero, as no particles will interact with others in the system anymore.
The idea of divirging particles seems strange, though it does point to some form of “time travel”. In Feynman diagrams, positrons, which diverge from electrons in their angles at creation, are depicted as “time travelling” electrons.

